Methods¶
Boltzmann Inversion¶
Boltzmann inversion provides a potential of mean force for a given degree of freedom.
Fig. 5 Flowchart demonstrating useful options of the tool¶
It is mostly used for deriving bonded interactions from canonical sampling of a single molecule in vacuum, e. g. for polymer coarse-graining, where it is difficult to separate bonded and non-bonded degrees of freedom [Tschoep:1998]. The non-bonded potentials can then be obtained by using iterative methods or force matching.
The main tool which can be used to calculate histograms, cross-correlate
coarse-grained variables, create exclusion lists, as well as prepare
tabulated potentials for coarse-grained simulations is csg_boltzmann. It parses the
whole trajectory and stores all information on bonded interactions in
memory, which is useful for interactive analysis. For big systems,
however, one can run out of memory. In this case csg_stat can be used which,
however, has a limited number of tasks it can perform (see
Setting files for an example on its usage).
Another useful tool is csg_map. It can be used to convert an atomistic
trajectory to a coarse-grained one, as it is discussed in
Trajectories.
To use csg_boltzmann one has to first define a mapping scheme. This is outlined
in Mapping files. Once the mapping scheme is specified, it
is possible to generate an exclusion list for the proper sampling of the
atomistic resolution system.
Generating exclusion lists¶
Exclusion lists are useful when sampling from a special reference system is needed, for example for polymer coarse-graining with a separation of bonded and non-bonded degrees of freedom.
To generate an exclusion list, an atomistic topology without exclusions and a mapping scheme have to be prepared first. Once the .tpr topology and .xml mapping files are ready, simply run
csg_boltzmann --top topol.tpr --cg mapping.xml --excl exclusions.txt
This will create a list of exclusions for all interactions that are not
within a bonded interaction of the coarse-grained sub-bead. As an
example, consider coarse-graining of a linear chain of three beads which
are only connected by bonds. In this case, csg_boltzmann will create exclusions for
all non-bonded interactions of atoms in the first bead with atoms of the
3rd bead as these would contribute only to the non-bonded interaction
potential. Note that csg_boltzmann will only create the exclusion list for the fist
molecule in the topology.
To add the exclusions to the GROMACS topology of the molecule, either include the file specified by the –excl option into the .top file as follows
[ exclusions ]
#include "exclusions.txt"
or copy and paste the content of that file to the exclusions section of the GROMACS topology file.
Statistical analysis¶
For statistical analysis csg_boltzmann provides an interactive mode. To enter the
interactive mode, use the –trj option followed by the file name of
the reference trajectory
csg_boltzmann --top topol.tpr --trj traj.trr --cg mapping.xml
To get help on a specific command of the interactive mode, type
help <command>
for example
help hist
help hist set periodic
Additionally, use the
list
command for a list of available interactions. Note again that csg_boltzmann loads the
whole trajectory and all information on bonded interactions into the
memory. Hence, its main application should be single molecules. See the
introduction of this chapter for csg_stat the command.
If a specific interaction shall be used, it can be referred to by
molecule:interaction-group:index
Here, molecule is the molecule number in the whole topology,
interaction-group is the name specified in the <bond> section of
the mapping file, and index is the entry in the list of
interactions. For example, 1:AA-bond:10 refers to the 10th bond
named AA-bond in molecule 1. To specify a couple of interactions
during analysis, either give the interactions separated by a space or
use wildcards (e.g. *:AA-bond*).
To exit the interactive mode, use the command q.
If analysis commands are to be read from a file, use the pipe or stdin redirects from the shell.
cat commands | csg_boltzmann topol.top --trj traj.trr --cg mapping.xml
Distribution functions and tabulated potentials¶
Distribution functions (tabulated potentials) can be created with the
hist (tab) command. For instance, to write out the distribution
function for all interactions of group AA-bond (where AA-bond is the
name specified in the mapping scheme) to the file AA.txt, type
hist AA.txt *:AA-bond:*
The command
hist set
prints a list of all parameters that can be changed for the histogram:
the number n of bins for the table, bounds min and max for
table values, scaling and normalizing, a flag periodic to ensure
periodic values in the table and an auto flag. If auto is set to
1, bounds are calculated automatically, otherwise they can be specified
by min and max. Larger values in the table might extend those
bounds, specified by parameter extend.
To directly write the Boltzmann-inverted potential, the tab command
can be used. Its usage and options are very similar to the hist
command. If tabulated potentials are written, special care should be
taken to the parameters T (temperature) and the scale. The
scale enables volume normalization as given in
the equations in the theory section. Possible
values are no (no scaling), bond (normalize bonds) and angle
(normalize angles). To write out the tabulated potential for an angle potential
at a temperature of 300K, for instance, type:
tab set T 300
tab set scale angle
tab angle.pot *:angle:*
The table is then written into the file angle.pot in the format
described in Table formats. An optional correlation analysis
is described in the next section. After the file has been created by
command tab, the potential is prepared for the coarse-grained run in
Preparing coarse-grained runs.
Correlation analysis¶
The factorization of \(P\), as shown in the theory
section, assumed uncorrelated quantities. csg_boltzmann
offers two ways to evaluate correlations of interactions. One option is to use
the linear correlation coefficient (command cor).
However, this is not a good measure since cor calculates the linear
correlation only which might often lead to misleading
results [Ruehle:2009.a]. An example for such a case
are the two correlated random variables \(X \sim U[-1,1]\) with
uniform distribution, and \(Y:=X^2\). A simple calculation shows
\(cov(X,Y)=0\) and therefore
A better way is to create 2D histograms. This can be done by specifying all values (e.g. bond length, angle, dihedral value) using the command vals, e.g.:
vals vals.txt 1:AA-bond:1 1:AAA-angle:A
This will create a file which contains 3 columns, the first being the time, and the second and third being bond and angle, respectively. Columns 2 and 3 can either be used to generate the 2D histogram, or a simpler plot of column 3 over 2, whose density of points reflect the probability.
Two examples for 2D histograms are shown below: one for the propane molecule and one for hexane.
Fig. 6 propane histogram¶
Fig. 7 hexane histograms: before and after the coarse-grained run¶
The two plots show the correlations between angle and bondlength for both molecules. In the case of propane, the two quantities are not correlated as shown by the centered distribution, while correlations exist in the case of hexane. Moreover, it is visible from the hexane plot that the partition of the correlations has changed slightly during coarse-graining.
The tabulated potentials created in this section can be further modified and prepared for the coarse-grained run: This includes fitting of a smooth functional form, extrapolation and clipping of poorly sampled regions. Further processing of the potential is decribed in Preparing coarse-grained runs.
Force matching¶
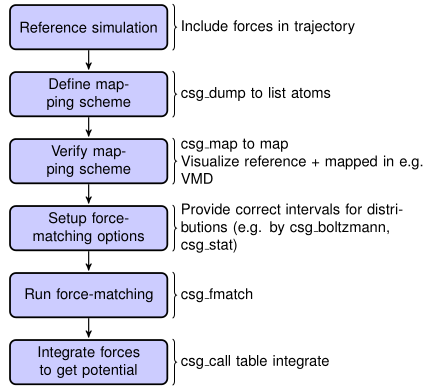
Fig. 8 Flowchart to perform force matching.¶
The force matching algorithm with cubic spline basis is implemented in
the utility. A list of available options can be found in the reference
section of (command –h).
Program input¶
csg_fmatch needs an atomistic reference run to perform coarse-graining. Therefore,
the trajectory file must contain forces (note that there is a suitable
option in the GROMACS .mdp file), otherwise csg_fmatch will not be able to
run.
In addition, a mapping scheme has to be created, which defines the
coarse-grained model (see Input files). At last, a control
file has to be created, which contains all the information for
coarse-graining the interactions and parameters for the force-matching
run. This file is specified by the tag –options in the XMLformat. An
example might look like the following
<cg>
<!--fmatch section -->
<fmatch>
<!--Number of frames for block averaging -->
<frames_per_block>6</frames_per_block>
<!--Constrained least squares?-->
<constrainedLS>false</constrainedLS>
</fmatch>
<!-- example for a non-bonded interaction entry -->
<non-bonded>
<!-- name of the interaction -->
<name>CG-CG</name>
<type1>A</type1>
<type2>A</type2>
<!-- fmatch specific stuff -->
<fmatch>
<min>0.27</min>
<max>1.2</max>
<step>0.02</step>
<out_step>0.005</out_step>
</fmatch>
</non-bonded>
</cg>
Similarly to the case of spline fitting (see Programs on
csg_resample), the parameters min and max have to be chosen in such a way as
to avoid empty bins within the grid. Determining min and max by
using csg_stat is recommended (see Setting files). A full description
of all available options can be found in Settings file.
Program output¶
csg_fmatch produces a separate .force file for each interaction, specified in
the CG-options file (--options). These files have 4 columns
containing distance, corresponding force, a table flag and the force
error, which is estimated via a block-averaging procedure. If you are
working with an angle, then the first column will contain the
corresponding angle in radians.
To get table-files for GROMACS, integrate the forces in order to get potentials and do extrapolation and potentially smoothing afterwards.
Output files are not only produced at the end of the program execution,
but also after every successful processing of each block. The user is
free to have a look at the output files and decide to stop csg_fmatch, provided
the force error is small enough.
Integration and extrapolation of .force files¶
To convert forces (.force) to potentials (.pot), tables have to
be integrated. To use the built-in integration command from the
scripting framework, execute
csg_call table integrate CG-CG.force minus_CG-CG.pot
csg_call table linearop minus_CG-CG.d CG-CG.d -1 0
This command calls the table_integrate.pl script, which integrates the force and writes the
potential to the .pot file.
In general, each potential contains regions which are not sampled. In this case or in the case of further post-processing, the potential can be refined by employing resampling or extrapolating methods. See Post-processing of the potential for further details.
Three-body Stillinger-Weber interactions¶
As described in the theory section, csg_fmatch is also able to parametrize
the angular part of three-body interactions of the Stillinger-Weber type (see subsec. Three-body Stillinger-Weber interactions).
The general procedure is the same, as shown in the two-body case
(See flowchart in Fig. Flowchart to perform force matching.).
It has to be specified in the control file that one wants to parametrize a three-body interaction. An example might look like this:
<cg>
<!-- fmatch section -->
<fmatch>
<!-- Number of frames for block averaging -->
<frames_per_block>10</frames_per_block>
<!-- Constrained least squares?-->
<constrainedLS>true</constrainedLS>
</fmatch>
<!-- example for a non-bonded interaction entry with three-body SW interactions -->
<non-bonded>
<!-- name of the interaction -->
<name>CG-CG-CG</name>
<!-- flag for three-body interactions -->
<threebody>true</threebody>
<!-- CG bead types (according to mapping file) -->
<type1>A</type1>
<type2>A</type2>
<type3>A</type3>
<!-- fmatch section of interaction -->
<fmatch>
<!-- short-range cutoff (in nm) -->
<a>0.37</a>
<sigma>1.0</sigma>
<!-- switching range (steepness of exponential switching function) (in nm) -->
<gamma>0.08</gamma>
<!-- min for angular interaction (in rad) -->
<min>0.7194247283</min>
<!-- max for angular interaction (in rad) -->
<max>3.1415927</max>
<!-- step size for internal spline representation (in rad) -->
<step>0.1</step>
<!-- output step size for angular interaction (in rad) -->
<out_step>0.0031415927</out_step>
</fmatch>
</non-bonded>
</cg>
As in the case of pair interactions, the parameters min and max have to be chosen in such a
way as to avoid empty bins within the grid. Determining min and max by using
csg_stat is recommended (see sec. Setting files).
For each three-body interaction as specified in the CG-options file
--options, csg_fmatch produces a separate .force file, as well as a
.pot file. Due to the functional form of the Stillinger-Weber potential,
csg_fmatch outputs the three-body force in angular direction, as well as the angular potential.
Therefore, in contrast to the two-body force (see section Integration and extrapolation of .force files), the angular
three-body force does not have to be numerically integrated. The .force, as well as
the .pot file have 4 columns containing the angle in radians, the force or potential,
the error (which is estimated via a block-averaging procedure) and a table flag.
Coarse-grained simulations with three-body Stillinger-Weber interactions can be done with
LAMMPS with the MANYBODY pair_style sw/angle/table (https://docs.lammps.org/pair_sw_angle_table.html). For this, the .pot file has to be
converted into a table format according to the LAMMPS angle_style table (https://docs.lammps.org/angle_table.html). This can be done with:
csg_call --options table.xml --ia-name XXX --ia-type angle convert_potential lammps --clean --no-shift XXX.pot table_XXX.txt
in line with the conversion of angular tables for bonded interactions. Therefore, the
CG-options file (--options) now has to contain a <bonded>
section with the appropriate interaction name:
<cg>
<bonded>
<!-- name of the interaction -->
<name>CG-CG-CG</name>
<!-- CG bead types (according to mapping file) -->
<type1>A</type1>
<type2>A</type2>
<type3>A</type3>
<min>0.7194247283</min>
<max>3.1415927</max>
<step>0.0031415927</step>
<!-- settings for converting table to lammps angular format -->
<inverse>
<lammps>
<table_begin>0</table_begin>
<table_end>180</table_end>
<table_bins>0.18</table_bins>
<y_scale>0.239006</y_scale>
<avg_points>1</avg_points>
</lammps>
</inverse>
</bonded>
</cg>
For a further description of posprocessing, we refer again to sec. Post-processing of the potential. For a more detailed example, we refer to the tutorial in csg-tutorials/spce/3body_sw/.
Iterative methods¶
The following sections deal with the Iterative Boltzmann Inversion (IBI) method, the Inverse Monte Carlo (IMC) method, the Iterative Integral Equation (IIE) method, and the Relative Entropy (RE) method.
Fig. 9 Flowchart of the spanning workflow of iterative methods.¶
In general, IBI, IMC, IIE, and RE are implemented within the same framework. Therefore, most of the settings and parameters used by these methods are similar and thus described in a general section (see Preparing the run). Further information on iterative methods follows in the next chapters, in particular on the IBI, IMC, IIE, and RE methods.
Iterative workflow control¶
Iterative workflow control is essential for the IBI, IMC, IIE, and RE methods.
Fig. 10 Forkflow control for the iterative methods. The most time-consuming parts are marked in red.¶
The general idea of iterative workflow is sketched in the flowchart above. During the global initialization the initial guess for the coarse-grained potential is calculated from the reference function or converted from a given potential guess into the internal format. The actual iterative step starts with an iteration initialization. It searches for possible checkpoints and copies and converts files from the previous step and the base directory. Then, the simulation run is prepared by converting potentials into the format required by the external sampling program and the actual sampling is performed.
After sampling the phasespace, the potential update is calculated. Often, the update requires postprocessing, such as smoothing, interpolation, extrapolation or fitting to an analytical form.
Finally, the new potential is determined and postprocessed. If the iterative process continues, the next iterative step will start to initialize.
How to start:¶
The first thing to do is generate reference distribution functions. These might come from experiments or from atomistic simulations. To get reasonable results out of the iterative process, the reference distributions should be of good quality (little noise, etc).
VOTCA can create initial guesses for the coarse-grained potentials by
Boltzmann inverting the distribution function. If a custom initial guess
for an interaction shall be used instead, the table can be provided in
<interaction>.pot.in. As already mentioned,
VOTCA automatically creates potential tables to run a simulation.
However, it does not know how to run a coarse-grained simulation.
Therefore, all files needed to run a coarse-grained simulation, except
for the potentials that are iteratively refined, must be provided and
added to the <filelist> in the settings XML-file. If an atomistic topology and a
mapping definition are present, VOTCA offers tools to assist the setup of
a coarse-grained topology (see Preparing coarse-grained runs).
To get an overview of how input files look like, it is suggested to take a look at one of the tutorials provided in csg_tutorials.
In what follows we describe how to set up the iterative coarse-graining, run the main script, continue the run, and add customized scripts.
Preparing the run¶
To start the first iteration, one has to prepare the input for the
sampling program. This means that all files for running a coarse-grained
simulation must be present and described in a separate XMLfile, in our
case settings.xml (see Setting files for details). An
extract from this file is given below. The only exception are tabulated
potentials, which will be created and updated by the script in the
course of the iterative process.
The input files include: target distributions, initial guess (optional)
and a list of interactions to be iteratively refined. As a target
distribution, any table file can be given (e.g. GROMACS output from
g_rdf). The program automatically takes care to resample the table
to the correct grid spacing according to the options provided in
settings.xml.
The initial guess is normally taken as a potential of mean force and is
generated by Boltzmann-inversion of the corresponding distribution
function. It is written in step_000/<name>.pot.new. If you want to
manually specify the initial guess for a specific interaction, write the
potential table to a file called <name>.pot.in in the folder where
you plan to run the iterative procedure.
A list of interactions to be iteratively refined has to be given in the
options file. As an example, the setting.xml file for a propane is
shown in below:
<cg>
<non-bonded> <!-- non-bonded interactions -->
<name>A-A</name> <!-- name of the interaction -->
<type1>A</type1> <!-- types involved in this interaction -->
<type2>A</type2>
<min>0</min> <!-- dimension + grid spacing of tables-->
<max>1.36</max>
<step>0.01</step>
<inverse>
<target>A-A.dist.tgt</target> <!-- target distribution -->
<do_potential>1 0 0</do_potential> <!-- update cycles -->
<gromacs>
<table>table_A_A.xvg</table>
</gromacs>
</inverse>
</non-bonded>
<!-- ... more non-bonded interactions -->
<!-- general options for the inverse script -->
<inverse>
<kBT>1.6629</kBT> <!-- 300*0.00831451 gromacs units -->
<program>gromacs</program> <!-- use gromacs to sample -->
<gromacs> <!-- gromacs specific options -->
<equi_time>10</equi_time> <!-- ignore so many frames -->
<table_bins>0.002</table_bins> <!-- grid for table*.xvg -->
<pot_max>1000000</pot_max> <!-- cut the potential at value -->
<table_end>2.0</table_end> <!-- extend the tables to value -->
<topol>topol.tpr</topol> <!-- topology + trajectory files -->
<traj>traj.xtc</traj>
</gromacs>
<!-- these files are copied for each new run -->
<filelist>grompp.mdp topol.top table.xvg
table_a1.xvg table_b1.xvg index.ndx
</filelist>
<iterations_max>300</iterations_max> <!-- number of iterations -->
<method>ibi</method> <!-- inverse Boltzmann or inverse MC -->
<log_file>inverse.log</log_file> <!-- log file -->
<restart_file>restart_points.log</restart_file> <!-- restart -->
</inverse>
</cg>
For more details, see the full description of all options in Settings file.
Starting the iterative process¶
After all input files have been set up, the run can be started by
csg_inverse --options settings.xml
Each iteration is stored in a separate directory, named
step_<iteration>. step_000 is a special folder which contains
the initial setup. For each new iteration, the files required to run the
CG simulation (as specified in the config file) are copied to the
current working directory. The updated potentials are copied from the
last step, step_<n-1>/<interaction>.pot.new, and used as the new
working potentials step_<n>/<interaction>.pot.cur.
After the run preparation, all potentials are converted into the format
of the sampling program and the simulation starts. Once the sampling has
finished, analysis programs generate new distributions, which are stored
in <interaction>.dist.new, and new potential updates, stored in
<interaction>.dpot.new.
Before adding the update to the old potential, it can be processed in
the post_update step. For each script that is specified in the
postupdate, <interaction>.dpot.new is renamed to
<interaction>.dpot.old and stored in
<interaction>.dpot.<a-number> before the processing script is
called. Each processing script uses the current potential update
<interaction>.dpot.cur and writes the processed update to
<interaction>.dpot.new. As an example, a pressure correction is
implemented as a postupdate script within this framework.
After all postupdate scripts have been called, the update is added to
the potential and the new potential <interaction>.pot.new is
written. Additional post-processing of the potential can be performed in
the post_add step which is analogous to the post_update step
except for a potential instead of an update.
To summarize, we list all standard output files for each iterative step:
|
distribution functions of the current step |
|
the final potential update, created by |
|
for each postupdate script, the |
is created |
|
|
the current potential used for the actual run |
|
the new potential after the add step |
|
same as |
If a sub-step fails during the iteration, additional information can be found in the log file. The name of the log file is specified in the steering XMLfile.
Restarting and continuing¶
The interrupted or finished iterative process can be restarted either by
extending a finished run or by restarting the interrupted run. When the
script csg_inverse is called, it automatically checks for a file called done in
the current directory. If this file is found, the program assumes that
the run is finished. To extend the run, simply increase inverse.iterations_max in the settings
file and remove the file called done. After that, can be restarted,
which will automatically recognize existing steps and continue after the
last one.
If the iteration was interrupted, the script csg_inverse might not be able to
restart on its own. In this case, the easiest solution is to delete the
last step and start again. The script will then repeat the last step and
continue. However, this method is not always practical since sampling
and analysis might be time-consuming and the run might have only crashed
due to some inadequate post processing option. To avoid repeating the
entire run, the script csg_inverse creates a file with restart points and labels
already completed steps such as simulation, analysis, etc. The file name
is specified in the option inverse.restart_file. If specific actions should be redone, one
can simply remove the corresponding lines from this file. Note that a
file done is also created in each folder for those steps which have
been successfully finished.
Iterative Boltzmann Inversion¶
Input preparation¶
This section describes the usage of IBI, implemented within the scripting framework described in Iterative workflow control. It is suggested to get a basic understanding of this framework before proceeding.
To specify Iterative Boltzmann Inversion as algorithm in the script, add
ibi in the method section of the XMLsetting file as shown below.
<cg>
...
<inverse>
<method>ibi</method>
</inverse>
</cg>
Inverse Monte Carlo¶
In this section, additional options are described to run IMC coarse graining. The usage of IMC is similar to that of IBI, hence, understanding the scripting framework described above is also necessary.
WARNING: multicomponent IMC is still experimental!
General considerations¶
In comparison to IBI, IMC needs significantly more statistics to calculate the potential update [Ruehle:2009.a]. It is advisable to perform smoothing on the potential update. Smoothing can be performed as described in Runtime optimization. In addition, IMC can lead to problems related to finite size: for methanol, an undersized system proved to lead to a linear shift in the potential [Ruehle:2009.a]. It is therefore always necessary to check that the system size is sufficiently large and that runlength csg smoothing iterations are well balanced.
Correlation groups¶
Unlike IBI, IMC also takes cross-correlations of interactions into account in
order to calculate the update. However, it might not always be beneficial to
evaluate cross-correlations of all pairs of interactions. By specifying
<group> for each interaction, as shown in the xml snippet below, one can
define groups of interactions, amongst which cross-correlations are taken into
account. <group> can be any name.
<non-bonded>
<name>CG-CG</name>
<type1>CG</type1>
<type2>CG</type2>
...
<imc>
<group>solvent</group>
</imc>
</non-bonded>
Regularization¶
To use the regularized version of IMC a \(\lambda\) value \(>0\)
has to be set with imc.groupname.reg. If set to \(0\) (default value) the
unregularized version of IMC is applied.
<inverse>
<imc>
<default_reg>150</default_reg>
<solvent>
<reg>300</reg>
</solvent>
</imc>
</inverse>
Internal degrees of freedom¶
For internal degrees of freedom, one can apply the IBI method as a post update method.
<inverse>
<imc>
<group>none</group>
</imc>
<do_potential>0</do_potential>
<post_update>ibi</post_update>
</inverse>
Iterative Integral Equation methods¶
In this section, we describe some options that are relevant only to IIE methods.
General considerations¶
In comparison to IBI, IIE methods need RDF information on a longer range than the cut-off. This means one needs a sufficiently large box or one can try the RDF extension method.
Currently, the methods do not allow more than one bead-type, albeit they allow for molecular CG representations.
Closure and optimization method¶
The initial guess can be table, Boltzmann Inversion (BI), or integral equation (IE). Three optimization methods are implemented: Newton, Newton-mod, and Gauss-Newton. The former two are very similar. With the latter constraints can be added. Two closures relations are implemented: hypernetted-chain (HNC) and Percus-Yevick (PY). The options in the xml file have to be lowercase.
<inverse>
...
<iie>
<initial_guess>
<method>ie</method>
<closure>hnc</closure>
</initial_guess>
<method>newton</method>
<closure>hnc</closure>
...
</iie>
</inverse>
Pressure constraint¶
When using the Gauss-Newton method one can impose a pressure constraint (in bar). This can lead to instabilities in the core region of the potential and make an extrapolation necessary. There is also an option to fix steps near the cut-off.
<inverse>
...
<iie>
<method>gauss-newton</method>
...
<pressure_constraint>1.0</pressure_constraint>
<extrap_near_core>constant</extrap_near_core>
<fix_near_cut_off>none</fix_near_cut_off>
</iie>
</inverse>
Other options¶
One can set a a cut-off for the potential, which can (and should) be lower than the range of the RDF. Number densities of the CG beads have to be provided. The RDF can be extrapolated by a built-in algorithm but the result should be validated to be meaningful. One can choose to ignore the RISM formalism for the case of bonds in the CG representation (not recommended). The number of beads per molecule has to be provided.
<inverse>
...
<iie>
...
<cut_off>1.2</cut_off>
<densities>4.651</densities>
<g_extrap_factor>2</g_extrap_factor>
<ignore_intramolecular_correlation>false</ignore_intramolecular_correlation>
<n_intra>4</n_intra>
</iie>
</inverse>
Relative Entropy¶
In this section, additional options are described to run RE coarse graining. The usage of RE is similar to that of IBI and IMC and understanding the use of the scripting framework described in Iterative workflow control is necessary.
Currently, RE implementation supports optimization of two-body non-bonded pair interactions. Support for bonded and N-body interactions is possible by further extension of RE implementation.
Potential function and parameters¶
In RE, CG potentials are modeled using analytical functional forms. Therefore, for each CG interaction, an analytical functional must be specified in the XMLsetting file as
<non-bonded>
<name>CG-CG</name>
<type1>CG</type1>
<type2>CG</type2>
...
<re>
<function>cbspl or lj126</function>
<cbspl>
<nknots>48</nknots>
</cbspl>
</re>
...
</non-bonded>
Currently, standard Lennard-Jones 12-6 (lj126) and uniform cubic B-splines-based piecewise polynomial (cbspl) functional forms are supported. For lj126, the parameters to optimize are the usual \(C_{12}\) and \(C_{6}\). The cbspl form is defined as
where \(\{c_0,c_1,c_2,...,c_m\}\) are the spline knot values tabulated for \(m\) evenly spaced intervals of size \(\Delta r = r_{\text{cut}}/(m-2)\) along the separation distance \(r_{i} = i\times\Delta r\) with the cut-off \(r_{\text{cut}}\), and \(t\) is given by
where index \(k\) is determined such that \(r_{k}\leq r < r_{k+1}\). For cbspl, the knot values, \(\{c_0,c_1,c_2,...,c_m\}\), are optimized. The number of knot values to use must be specified in the XMLsetting file as shown in the above snippet. \(u_{\text{cbspl}}(r)\) exhibits remarkable flexibility, and it can represent various complex functional characteristics of pair potentials for sufficiently large number of knots.
Update scaling parameter¶
Depending on the quality of the initial guess and sensitivity of the CG system to the CG parameters, scaling of the parameter update size may be required to ensure the stability and convergence of the RE minimization. The scaling parameter, \(\chi\in(0...1)\), value can be specified in the XMLsettings file.
Statistical averaging of parameters¶
Due to stochastic nature of the CG simulations, near convergence, the CG
potential paramters may fluctuate around the mean converged values.
Therefore, the optimal CG parameters can be estimated by averaging over
the last few iterations. To specify averaging, the <average>, keyword
should be specified in the <post_update> options in the XMLsettings
file.
General considerations¶
To ensure the stability of the relative entropy minimization, some precautionary measures are taken. For the Newton-Raphson update to converge towards a minimum, the Hessian, \(\mathbf{H}\), must be positive definite at each step. With a good initial guess for the CG parameters and by adjusting the value of the relaxation parameter, \(\chi\), stability of the Newton-Raphson method can be ensured. One approach to initialize the CG parameters can be to fit them to PMF obtained by inverting the pair distributions of the CG sites obtained from the reference AA ensemble. For the lj126 and cbspl forms, which are linear in its parameters, the second derivative of \(S_{\text{rel}}\) is never negative, hence the minimization converges to a single global minimum. However, due to locality property of the cbspl form, i.e., update to \(c_i\) affects only the value of the potential near \(r_i\), and the poor sampling of the very small separation distances in the high repulsive core, the rows of \(\mathbf{H}\) corresponding to the first few spline knots in the repulsive core may become zero causing \(\mathbf{H}\) to be a singular matrix. To avoid this singularity issue, we specify a minimum separation distance, \(r_{\text{min}}\), for each CG pair interaction and remove the spline knots corresponding to the \(r\le r_{\text{min}}\) region from the Newton-Raphson update. Once the remaining knot values are updated, the knot values in the poorly sampled region, i.e., \(r\le r_{\text{min}}\), are linearly extrapolated. The value of \(r_{\text{min}}\) at each iteration is estimated from the minimum distance at which the CG RDF from the CG-MD simulation is nonzero. Also, to ensure that the CG pair potentials and forces go smoothly to zero near \(r_{\text{cut}}\), 2 knot values before and after \(r_{\text{cut}}\), i.e., total 4, are fixed to zero.
Pressure correction¶
The pressure of the coarse-grained system usually does not match the
pressure of the full atomistic system. This is because iterative
Boltzmann inversion only targets structural properties but not
thermodynamic properties. In order correct the pressure in such a way
that it matches the target pressure (inverse.p_target)., different strategies have been
used based on small modifications of the potential. The correction can
be enable by adding pressure to the list of inverse.post_update scripts. The type of
pressure correction is selected by setting inverse.post_update_options.pressure.type.
Simple pressure correction¶
In ref. [Reith:2003] a simple linear attractive potential was added to the coarse-grained potential
with prefactor \(A\)
\(\Delta p=P_i-P_\text{target}\), and scaling factor \(f\) and
\(P_\text{target}\) can be specified in the settings file as
inverse.post_update_options.pressure.simple.scale and
inverse.p_target.
As an example for a block doing simple pressure correction, every third interaction is
<post_update>pressure</post_update>
<post_update_options>
<pressure>
<type>simple</type>
<do>0 0 1</do>
<simple>
<scale>0.0003</scale>
</simple>
</pressure>
</post_update_options>
Here, inverse.post_update_options.pressure.simple.scale
is the scaling factor \(f\). In order to get the correct
pressure it can become necessary to tune the scaling factor \(f\)
during the iterative process.
Advanced pressure correction¶
In [Wang:2009] a pressure correction based on the virial expression of the pressure was introduced. The potential term remains as in the simple form while a different sturcture of the \(A\) factor is used:
This factor requires the particle density \(\rho\) as additional
input parameter, which is added as inverse.particle_dens in the input file.
Kirkwood-Buff correction¶
In order to reproduce the exact Kirkwood-Buff ingetrals (KBIs), an correction term can be added into the coarse-grained potential [Ganguly:2012],
where \(G_{ij}^{(ref)}\) is the KBI calculated from the reference all-atom simulation and \(G_{ij}^{(n)}\) is the KBI after the \(n^{th}\) iteration.
The Kirkwood-Buff integrals are calculated from the radial distribution functions as follows:
For simulations of finite box size we calculate the running integral up to distance \(R\)
The average of those running integrals in the interval, where \(G_{ij}(R)\) gets flat, gives a good estimate for \(G_{ij}\):
As an example for a block doing Kirkwood-Buff correction, every iteraction without doing potential update
<do_potential>0</do_potential>
<post_update>kbibi</post_update>
<post_update_options>
<kbibi>
<do>1</do>
<start>1.0</start>
<stop>1.4</stop>
<factor>0.05</factor>
<r_ramp>1.4</r_ramp>
</kbibi>
</post_update_options>
Here, inverse.post_update_options.kbibi.factor is the scaling factor \(A\).
inverse.post_update_options.kbibi.start is \(r_1\)
and inverse.post_update_options.kbibi.stop is \(r_2\)
used to calculate the average of \(G_{ij}(R)\).
Runtime optimization¶
Most time per iteration is spent on running the coarse-grained system and on calculating the statistics. To get a feeling on how much statistics is needed, it is recommended to plot the distribution functions and check whether they are sufficiently smooth. Bad statistics lead to rough potential updates which might cause the iterative refinement to fail. All runs should be long enough to produce distributions/rdfs of reasonable quality.
Often, runtime can be improved by smoothing the potential updates. Our experience has shown that it is better to smooth the potential update instead of the rdf or potential itself. If the potential or rdf is smoothed, sharp features like the first peak in SPC/Ewater might get lost. Smoothing on the delta potential works quite well, since the sharp features are already present from the initial guess. By applying iterations of a simple triangular smoothing \(\left(\Delta U_i = 0.25 \Delta U_{i-1} + 0.5\Delta U_i + 0.25\Delta U_{i+1}\right)\), a reasonable coarse-grained potential for SPC/Ewater could be produced in less than 10 minutes. Smoothing is implemented as a post_update script and can be enabled by adding
<post_update>smooth</post_update>
<post_update_options>
<smooth>
<iterations>2</iterations>
</smooth>
</post_update_options>
to the inverse section of an interaction in the settings XMLfile.
Coordination Iterative Boltzmann Inversion¶
The method \(\mathcal{C}-\)IBI (Coordination Iterative Boltzmann Inversion) uses pair-wise cumulative coordination as a target function within an iterative Boltzmann inversion. This method reproduces solvation thermodynamics of binary and ternary mixtures [deOliveira:2016].
The estimation of coordination is given by:
with the indices \(i\) and \(j\) standing for every set of pairs, uses a volume integral of \({\rm g}(r)\).
The Kirkwood and Buff theory (KB) [Kirkwood:1951] connects the pair-wise coordinations with particule fluctuations and, thus, with the solution thermodynamics [Mukherji:2013,Naim:2006]_. This theory make use of the Kirkwood-Buff integrals (KBI) \({\rm G}_{ij}\) defined as,
For big system sizes the \({\rm G}_{ij}\) can be approximated:
were the second therm is a volume correction to \(\mathcal{C}_{ij}(r)\).
Thus the initial guess for the potential of the CG model is obtained from the all atom simulations,
however, the iterative protocol is modified to target \(\mathcal{C}_{ij}(r)\) given by,
To perform the \(\mathcal{C}-\)IBI is necessary include some lines inside of the .xml file:
<cg>
<non-bonded>
<name>A-A</name>
...
<inverse>
<post_update>cibi</post_update>
<post_update_options>
<cibi>
<do>1</do>
</cibi>
</post_update_options>
...
</cg>